Introduction

In a recent paper, Bader, Yan, and Zhang (2017) claim that the asymptotic distribution of the score statistic is not the usual \(\chi^2_q\) distribution when \(r\) increases. They hint that this non-regularity is due to the fact that the support of the distribution depends on the parameter. This claim is misleading and the goal of this post is to show that regularity conditions hold in most settings.

Regularity conditions

For extreme value distributions, the \(k\)th order cumulants are undefined when the shape parameter \(\xi < -1/k\). This has practical implications: the likelihood function is unbounded whenever \(\xi < -1\), since there are combinations of the other parameters that drive the likelihood value towards infinity. If the maximum likelihood estimate (MLE) is on the boundary of the parameter space, such as when \(\xi=-1\), then the model does not solve the score equation and is not regular.

Second order cumulants exist only if \(\xi>-1/2\) so the Fisher information matrix is undefined in those cases. In particular, this implies that the Fisher information cannot be evaluated at \(\hat{\boldsymbol{\theta}}\) if \(\hat{\xi} < -1/2\) (since we plug-in \(\hat{\xi}\) in the equation) — this precludes the use of a score test. Maximum likelihood estimators for the generalized extreme value distribution are superefficient in the zone \(-1 < \xi < -1/2\) (Smith 1985).

The model is regular for all relevant purposes of testing if we exclude some regions where the shape is strongly negative. It does not matter in those cases whether the support depends on the parameters. The following simulation study illustrates this point.

Score test

The score test is used to test a restriction of the parameters \(\boldsymbol{\theta} = (\mu, \sigma, \xi) \in \Theta\) to a subspace \(\Theta_0 \subset \Theta\). For example, consider the null hypothesis \(\mathrm{H}_0: \xi = \xi_0\). Then, \[ \begin{align*} \Theta &=\{(\mu, \sigma, \xi) \in \mathbb{R} \times \mathbb{R}_{+} \times \mathbb{R}: \{1+\xi(z_i-\mu)/\sigma > 0\}\\ \Theta_0 &=\{(\mu, \sigma) \in \mathbb{R} \times \mathbb{R}_{+}: \{1+\xi_0(z_i-\mu)/\sigma > 0\}. \end{align*} \]
The test statistic is \(w_{\mathrm{score}} \equiv S(\mathbf{x}; \hat{\boldsymbol{\theta}}_0)^\top i^{-1}(\mathbf{x}; \hat{\boldsymbol{\theta}}_0)S(\mathbf{x}; \hat{\boldsymbol{\theta}}_0)\). Under the null hypothesis that imposes \(q\) restrictions, the null distribution is \(\chi^2_q\). The benefit of the score test, relative to the likelihood ratio test, is that we only need to obtain the maximum likelihood estimates under \(H_0\), \(\hat{\boldsymbol{\theta}}_0\). This feature is more relevant when the null is much simpler than the alternative, e.g., if the later is computationally untractable.

The first Bartlett identity implies that the score has expectation zero at the true parameter value, meaning that \(\mathrm{E}(S(\boldsymbol{X}; \boldsymbol{\theta}); \boldsymbol{\theta})=0\) for all \(\boldsymbol{\theta} \in \Theta\). The maximum likelihood estimate solves the score vector, \(S(\mathbf{x}; \hat{\boldsymbol{\theta}})=0\). This property can be used to verify that the optimization routine has converged.

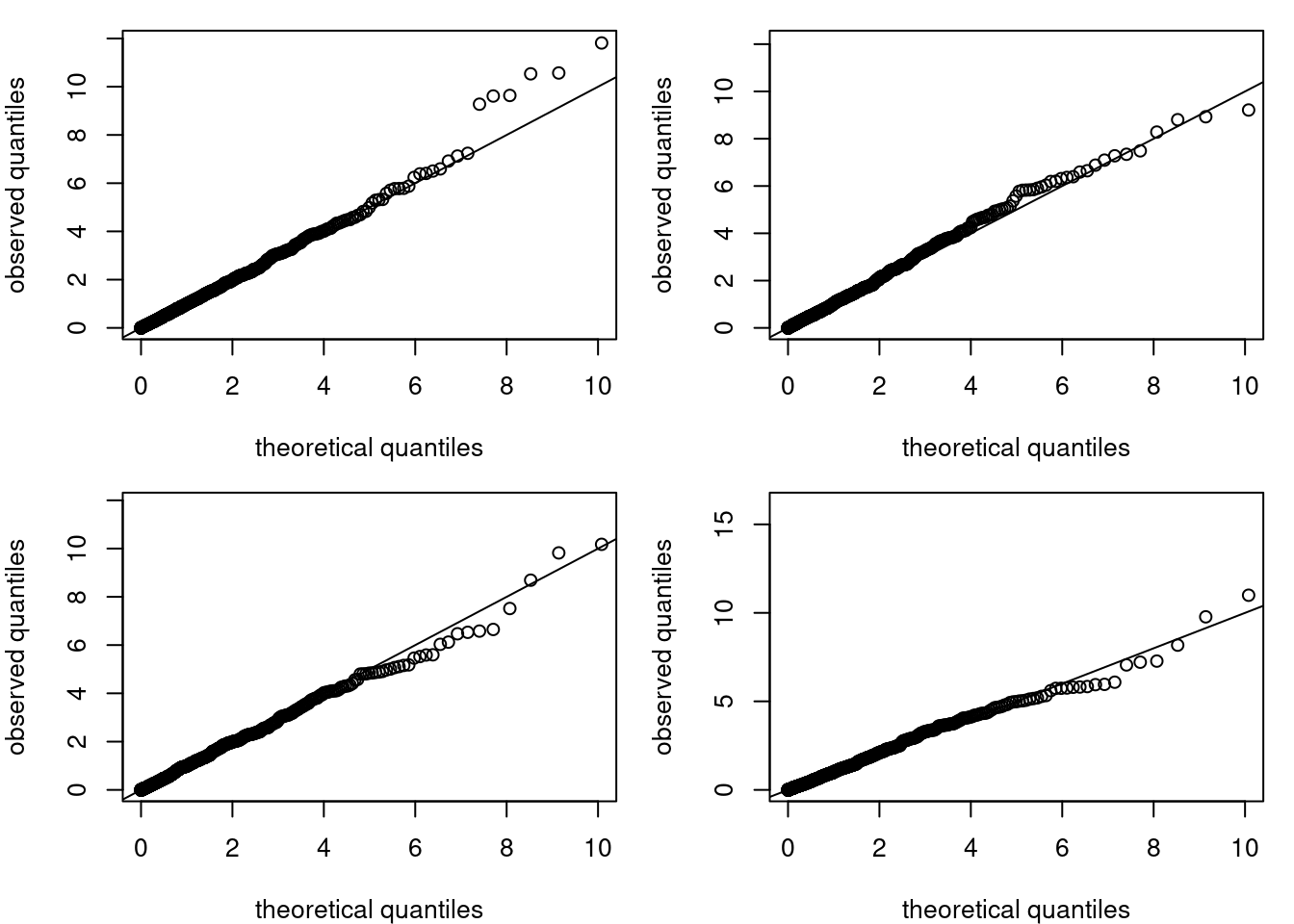
Below, I consider a restriction of \(\mathrm{H}_0: \xi=0.1\) and simulate realizations of the score statistic under the null hypothesis.

Figure 1: \(\chi^2_1\) quantile-quantile plots of the score test statistic \(w_{\mathsf{score}}\) based on \(1000\) independent replicates of the score test statistic computed on a sample size \(n=5000\) with \(r=1, 3, 5, 10\) for the true null hypothesis \(\xi=0.1\).

The empirical distribution of the test statistic in Figure 1 matches the asymptotic \(\chi^2_1\) distribution, independent of the value of \(r\).

References

Bader, Brian, Jun Yan, and Xuebin Zhang. 2017. “Automated Selection of \(r\) for the \(r\) Largest Order Statistics Approach with Adjustment for Sequential Testing.” Statistics and Computing 27 (6): 1435–51. https://doi.org/10.1007/s11222-016-9697-3.

Smith, Richard L. 1985. “Maximum Likelihood Estimation in a Class of Nonregular Cases.” Biometrika 72 (1): 67–90. https://doi.org/10.1093/biomet/72.1.67.

Citation

BibTeX citation:

@online{belzile2019,
  author = {Belzile, Léo},
  title = {Regularity of Asymptotics for Extreme Value Distributions},
  date = {2019-07-09},
  url = {https://lbelzile.bitbucket.io/posts/regularity-rlargest},
  langid = {en}
}

For attribution, please cite this work as:

Belzile, Léo. 2019. “Regularity of Asymptotics for Extreme Value Distributions.” July 9, 2019. https://lbelzile.bitbucket.io/posts/regularity-rlargest.